Loops and Nearest neighbor rules

Next: Constrained folding Up: Algorithms and Thermodynamics for Previous: Software platforms and environment

Loops and Nearest neighbor rules

The mfold software uses what are called nearest neighbor energy rules. That is, free energies are assigned to loops rather than to base pairs. These have also been called loop dependent energy rules. In an effort to keep this article as self-contained as possible, we are including some well-known definitions that may be found elsewhere [21,22,23].

A secondary structure, S on an RNA sequence, ${\bf R} = r_1,r_2,r_3,\dots,r_n$ , is a set of base pairs. A base pair between nucleotides r_i and r_j (i<j) is denoted by i.j. A few constraints are imposed.

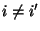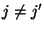Two base pairs, i.j and i'.j' are either identical, or else $i \neq i'$ and $j \neq j'$ . Thus base triples are deliberately excluded from the definition of secondary structure.
Sharp U-turns are prohibited. A U-turn, called a hairpin loop, must contain at least 3 bases.
Pseudoknots are prohibited. That is, if i.j and 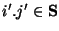$i'.j' \in {\bf S}$ , then, assuming i < i', either i < i' < j' < j or i < j < i' < j'.

Pseudoknots [24, 25, 26, 27, 28,29] and base triples are not excluded for frivolous reasons. When pseudoknots are included, the loop decomposition of a secondary structure breaks down and the energy rules break down. Although we can assign reasonable free energies to the helices in a pseudoknot, and even to possible coaxial stacking between them, it is not possible to estimate the effects of the new kinds of loops that are created. Base triples pose an even greater challenge, because the exact nature of the triple cannot be predicted in advance, and even if it could, we have no data for assigning free energies.

A base r_i' or a base pair i'.j' is called accessible from a base pair i.j if i < i' ( < j') < j and if there is not other base pair, k.l such that i < k < i' ( < j' ) < l < j. The collection of bases and base pairs accessible from a given base pair, i.j, but not including that base pair, is called the loop closed by i.j. We denote it by L(i.j). The collection of bases and base pairs not accessible from any base pair is called the exterior (or external) loop, and will be denoted by L_e here. It is worth noting that if we imagine adding a 0^th and an (n+1)^stbase to the RNA, and a base pair 0.(n+1), then the exterior loop becomes the loop closed by this imaginary base pair. We call this the universal closing base pair of an RNA structure. If S is a secondary structure, then S' denotes the same secondary structure with the addition of the universal closing base pair. The exterior loop exists only in linear RNA. It is treated differently than other loops because we assume as a first approximation that there are no conformational constraints, and therefore no associated entropic costs.

Any secondary structure, S decomposes an RNA uniquely into loops. We can write this as:

R =

∪
i.j ∈ S′

L(i.j)

Loops may contain 0, 1 or more base pairs. The term k-loop denotes a loop containing k-1 base pairs, making a total of k base pairs by including the closing base pair. We introduce the terms l_s(L) and l_d(L) to denote the number of single-stranded bases and base pairs in a loop, respectively. The size of a 1 or 2-loop is defined as l_s(L).

A 1-loop is called a hairpin loop. Polymer theory predicts that the free energy increment δδG for such a loop is given by

δδG = 1.75RTln(l_s),

(1)

where T is absolute temperature and R is the universal gas constant (1.9872 cal/mol/K). The factor 1.75 would be 2 if the chain were not self-avoiding in space. In reality, we use tabulated values for δδG for l_s from 3 to 30. These values are based on measurements and interpolations of measurements, and are stored in an file named loop.dg, or loop.TC, where TC is a temperature (integral) in °C. We use the latter only when departing from our temperature standard of 37° C. Thus loop.dg and loop.37 refer to the same file. The same convention holds for other files defined below. Equation 1 is used to extrapolate beyond size 30. Thus, for l_s > 30,

δδG = δδG₃₀ + 1.75 RT ln ( l_s/30 ).

(2)

Figure 1 shows the information stored in the loop file.

**Figure 1:** The *loop.dg* or *loop.TC* contains size based free energy increments for hairpin, bulge and interior loops up to size 30. Entries with `.' are undefined.
DESTABILIZING ENERGIES BY SIZE OF LOOP (INTERPOLATE WHERE NEEDED) hp3 ave calc no tmm;hp4 ave calc with tmm; ave all bulges SIZE INTERNAL BULGE HAIRPIN ------------------------------------------------------- 1 . 3.8 . 2 . 2.8 . 3 . 3.2 5.6 4 1.7 3.6 5.5 5 1.8 4.0 5.6 6 2.0 4.4 5.3 7 2.2 4.6 5.8 8 2.3 4.7 5.4 ... 30 3.7 6.1 7.7

Figure 1: The loop.dg or loop.TC contains size based free energy increments for hairpin, bulge and interior loops up to size 30. Entries with `.' are undefined.

DESTABILIZING ENERGIES BY SIZE OF LOOP (INTERPOLATE WHERE NEEDED)
hp3 ave calc no tmm;hp4 ave calc with tmm; ave all bulges
SIZE         INTERNAL          BULGE            HAIRPIN
-------------------------------------------------------
1               .                3.8               . 
2               .                2.8               . 
3               .                3.2              5.6
4              1.7               3.6              5.5
5              1.8               4.0              5.6
6              2.0               4.4              5.3
7              2.2               4.6              5.8
8              2.3               4.7              5.4
 ...
30             3.7               6.1              7.7

**Figure 2:** On the left, a typical 4 × 4 table. The pairs WX and YZ are covalently linked. WZ is assumed to be the closing base pair of a hairpin loop, and XY is the mismatched pair. `X' refers to row , and `Y' to column, in order A, C, G and U. Thus `aGU' is the same as `a34' and is the mismatch free energy for a GU mismatch (X=G and Y=U). On the right is a sample table for W=C and Z=G.
5' --> 3' 5' --> 3' WX CX ZY GY 3' <-- 5' 3' <-- 5' Y: A C G U A C G U ------------------ ----------------- X:A \| aAA aAC aAG aAU -1.5 -1.5 -1.4 -1.8 C \| aCA aCC aCG aCU -1.0 -0.9 -2.9 -0.8 G \| aGA aGC aGG aGU -2.2 -2.0 -1.6 -1.2 U \| aUA aUC aUG aUU -1.7 -1.4 -1.9 -2.0

Figure 2: On the left, a typical 4 × 4 table. The pairs WX and YZ are covalently linked. WZ is assumed to be the closing base pair of a hairpin loop, and XY is the mismatched pair. `X' refers to row , and `Y' to column, in order A, C, G and U. Thus `aGU' is the same as `a34' and is the mismatch free energy for a GU mismatch (X=G and Y=U). On the right is a sample table for W=C and Z=G.

         5' --> 3'              5' --> 3'               
            WX                     CX                   
            ZY                     GY                   
         3' <-- 5'              3' <-- 5'               
   Y: A    C    G    U       A    C    G    U           
    ------------------      -----------------           
X:A | aAA  aAC  aAG  aAU    -1.5 -1.5 -1.4 -1.8
  C | aCA  aCC  aCG  aCU    -1.0 -0.9 -2.9 -0.8
  G | aGA  aGC  aGG  aGU    -2.2 -2.0 -1.6 -1.2
  U | aUA  aUC  aUG  aUU    -1.7 -1.4 -1.9 -2.0

In addition, the effects of terminal mismatched pairs are taken into account for hairpin loops of size greater than 3. For loops of size 4 and greater closed by a base pair i.j, δδG is applied. This is referred to as the terminal mismatch free energy for hairpin loops. These parameters are stored in a file named tstackh.dg or tstackh.TC, as above. The data are arranged in 4×4 tables that each comprise 4 rows and columns. Figure 2 illustrates how the parameters are stored.

Both the loop and tstackh files treat hairpin loops in a generic way, and assume no special structure for the bases in the loop. We know that this is not true in general. For example, the anti-codon loop of tRNA is certainly not unstructured. For certain small hairpin loops, special rules apply. Hairpin loops of size 3 are called triloops and those of size 4 are called tetraloops. Files of distinguished triloops and tetraloops have been created to store the free energy bonus assigned to those loops. These parameters are stored in files triloop.dg and tloop.dg, respectively (or triloop.TC and tloop.TC for a specific temperature, TC). Some typical entries are given in Figure 3

**Figure 3:** Sample *distinguished* tetraloops together with the free energy bonuses, in kcal/mol, attached to them. These entries include the closing base pair of the loop. Triloops are not shown since they are not currently in use for RNA folding.
Seq Energy ------------- GGGGAC -3.0 ... CGAAGG -2.5 CUACGG -2.5 ... GUGAAC -1.5 UGGAAA -1.5

Finally, there are some special hairpin loop rules derived from experiments that will be defined explicitly here. A hairpin loop closed by r_i and r_j (i<j) called a "GGG" loop if r_i-2 = r_i-1 = r_i = G and r_j = U. Such a loop receives a free energy bonus that is stored in the miscloop.dg or miscloop.TC file, which contains a variety of miscellaneous, or extra free energy parameters. Another special case is the "poly-C" hairpin loop, where all the single stranded bases are C. If the loop has size 3, it is given a free energy penalty of c3. Otherwise, the penalty is c₂ + c₁ × l_s. The constants c₁, c₂ and c₃ are all stored in the miscloop file.

To summarize, we can write the free energy, δδG_H of a hairpin loop as:

δδG_H = δδG¹_H + δδG²_H + δδG³_H + δδG⁴,

(3)

where

δδG¹_H is the size dependent contribution from the loop file, or from equation 2 for sizes > 30,
δδG²₂ is the terminal mismatch stacking free energy, taken from the tstackh file (0 for hairpin loops of size 3),
δδG³_H is the bonus free energy for triloops or tetraloops listed in the TRILOOP or TLOOP files. This value is 0 for loops not listed in the TRILOOP or TLOOP files and for loop sizes > 4 and
δδG⁴_H is the bonus or penalty free energy for special cases not covered by the above.

A 2-loop, L is closed by a base pair i.j and contains a single base pair, i'.j', satisfying i < i' < j' < j. In this case, the loop size, l_s(L), can be written as:

l_s(L) = l_s¹(L) + l_s²(L),

where l_s¹(L) = i'-i-1 and l_s²(L) = j-j'-1.

A 2-loop of size 0 is called a stacked pair. This refers to the stacking between the i.j and immediately adjacent $i\!+\!1.j\!-\!1$ base pair contained in the loop. Free energies for these loops are stored in a file named stack.dg, or stack.TC, where TC is a temperature, as defined above. The layout is the same as for the tstackh file. A portion of such a file is given in Figure 4. A group of 2 or more consecutive base pairs is called a helix. The first and last are the closing base pairs of the helix. They may be written as i.j and i'.j', where i < i' < j' < j. Then i.j is called the external closing base pair and i'.j' is called the internal closing base pair. This nomenclature is used for circular RNA as well, even though it depends on the choice of origin.

**Figure 4:** Sample free energies in kcal/mol for CG base pairs stacked over all possible base pairs, XY. X refers to row and Y refers to column, in the order A, C, G and U respectively. Entries denoted by an isolated period, `.', are undefined, and may be considered as $+\infty$ .
5' --> 3' CX GY 3' <-- 5' Y: A C G U ---------------------- X:A \| . . . -2.1 C \| . . -3.3 . G \| . -2.4 . -1.4 U \| -2.1 . -2.1 .

Only Watson-Crick and wobble GU pairs are allowed as bona fide base pairs, even though the software is written to allow for any base pairs. The reason is that nearest neighbor rules break down for non-canonical, even GU base pairs, and that mismatches must instead be treated as small, symmetric interior loops. Note that the stacks 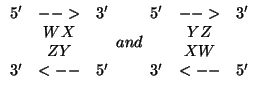$\begin{array}{ccc} 5' & --> & 3' \ & WX \ & ZY \ 3' & <-- & 5' \end{... ...in{array}{ccc} 5'& -->& 3' \ & YZ \ & XW \ 3' & <-- & 5' \end{array}$ are identical, and yet formally different for $W \neq Y$ and $X \neq Z$ . These stacked pairs are stored twice in the file, and the mfold software checks for symmetry. This is an example of built in redundancy as a check on precision.

A 2-loop, L of size > 0 is called a bulge loop if l_s¹(L) = 0 or l_s²(L) = 0 and an interior loop if both l_s¹(L) = 0 and l_s²(L) = 0.

Bulge loops up to size 30 are assigned free energies from the loop file (See Figure 1). For larger bulge loops, equation 2 is used. When a bulge loop has size 1, the stacking free energy for base pairs i.j and i'.j' are used (from the stack file).

Interior loops have size $\geq 2$ . If l_s¹(L) = l_s²(L), the loop is called symmetric; otherwise, it is asymmetric, or lopsided. The asymmetry of an interior loop, a(L) is defined by:

a(L) = | l_s¹(L) - l_s²(L) |

(4)

The free energy, $δδG_{I}$ , of an interior loop is the sum of 4 components:

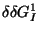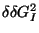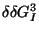$\begin{displaymath} δδG_{I} = δδG_{I}^{1} + δδG_{I}^{2} + δδG_{I}^{3} + δδG_{I}^{4}. \end{displaymath}$

(5)

$δδG_{I}^{1}$ is the size dependent contribution from the loop file, or from equation 2 for sizes > 30.
$δδG_{I}^{2}$ and $δδG_{I}^{3}$ are terminal mismatch stacking free energies, taken from the tstacki file. The format of this file is identical to the format of the tstackh file. There are 2 terms because of the terminal stacking of both r_i+1 and r_j-1on the i.j base pair, and of both r_i'-1 and r_j'+1 on the i'.j' base pair. This may be visualized as

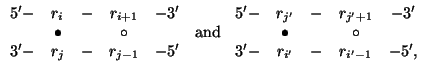
$\displaystyle \begin{array}{ccccc} {\rm 5'}-&r_{i}&-&r_{i+1}&-{\rm 3'} \ & \b... ... \ & \bullet & & \circ \ {\rm 3'}-&r_{i'}&-&r_{i'-1}&-{\rm 5'}, \end{array}$

where $\bullet$ denotes a base pair and $\circ$ denotes a mismatched pair.
$δδG_I⁴ is the asymmetry penalty, and is a function of a(L) defined in equation 4. The penalty is 0 for symmetric interior loops. The asymmetric penalty free energies come from the miscloop.dg or miscloop.TC file.

Equation 5 is now used only for loops of size > 4 or of asymmetry > 1. This means that special rules apply to 1×1 1×2 and 2×2 interior loops. Free energies for these symmetric and almost symmetric interior loops are stored in files sint2.dg, asint1x2.dg and sint4.dg, respectively. As above, the suffix TC is used in place of dg when explicit attention is paid to temperature. These files list all possible values of the single stranded bases, and all possible Watson-Crick and GU base pair closings. The sint2 file comprises a 6 × 6 array of 4 × 4 tables. There is a table for all possible 6 × 6 closing base pairs. The free energy values for each choice of closing base pairs are arranged in 4 × 4 tables. The term "closing base pairs" refers to the closing base pair of the loop and the contained base pair of the loop, as in the strict definition of a loop. An example of such a table is given in Figure 5.

**Figure 5:** Left: Free energies for all 1 × 1 interior loops in DNA closed by a CG and an AT base pair. Right: Free energies for all 1 × 2 interior loops in RNA closed by a CG and an AU base pair, with a single stranded U 3' to the double stranded U. As in similar Figures, X refers to row and Y to column.
5' --> 3' 5' --> 3' X X C A C A G T G U Y YA 3' <-- 5' 3' <-- 5' Y: A C G T Y: A C G U --------------------- --------------------- X:A \| 1.1 2.1 0.8 1.0 X:A \| 3.2 3.0 2.4 4.8 C \| 1.7 1.8 1.0 1.4 C \| 3.1 3.0 4.8 3.0 G \| 0.5 1.0 0.3 2.0 G \| 2.5 4.8 1.6 4.8 T \| 1.0 1.4 2.0 0.6 U \| 4.8 4.8 4.8 4.8

Figure 5: Left: Free energies for all 1 × 1 interior loops in DNA closed by a CG and an AT base pair. Right: Free energies for all 1 × 2 interior loops in RNA closed by a CG and an AU base pair, with a single stranded U 3' to the double stranded U. As in similar Figures, X refers to row and Y to column.

          5' --> 3'                  5' --> 3'        
              X                          X            
             C A                        C  A
             G T                        G  U           
              Y                          YA            
          3' <-- 5'                  3' <-- 5'        
   Y:   A    C    G    T      Y:   A    C    G    U
   ---------------------      ---------------------   
X:A | 1.1  2.1  0.8  1.0   X:A | 3.2  3.0  2.4  4.8   
  C | 1.7  1.8  1.0  1.4     C | 3.1  3.0  4.8  3.0   
  G | 0.5  1.0  0.3  2.0     G | 2.5  4.8  1.6  4.8   
  T | 1.0  1.4  2.0  0.6     U | 4.8  4.8  4.8  4.8

The asint1x2 file comprises a 24 row by 6 column array of 4 × 4 tables. There is a 4 × 4 table for all possible 6 × 6 closing base pairs and choice of one of the single stranded bases. The free energy values for each choice of closing base pairs and a single stranded base are arranged in 4 × 4 tables. An example of these tables is given in Figure 5.

Finally, the sint4 file contains 36 16 × 16 tables, 1 for each pair of closing base pairs. A 2 × 2 interior loop can have 4⁴ combinations of single stranded bases. If, for example, the loop is closed by a GC base pair and an AU base pair, we can write it as:

  5' ------> 3'
   G \/ \_/ A
   C /\  |  U
  3' <------ 5'

Both the large `X' and large `Y' refer to an unmatched pair of bases that are juxtaposed. They can each take on 16 different values, from `AA',`AC', $\dots$ , to `UU', or 1 to 16, respectively. The number in row `X' and column `Y' of the table is the free energy of the 2 × 2 interior loop with the indicated single stranded bases. Figure 6 shows the full table for the CG and AU closing base pairs.

**Figure 6:** Free energies for all interior loops in RNA closed by a CG and an AU base pair. Values of `X' or `Y' that correspond to bases that could form Watson-Crick pairs have been removed for brevity.
5' ------> 3' C \/ \_/ A G /\ \| U 3' <------ 5' Y: A A A C C C G G G U U U A C G A C U A G U C G U -------------------------------------------------------------- AA 2.0 1.6 1.0 2.0 2.6 2.6 1.0 1.4 0.2 2.3 1.5 2.2 AC 2.4 1.9 1.3 2.4 2.4 2.4 1.3 1.7 -0.4 2.1 0.8 1.5 AG 0.9 0.4 -0.1 0.9 1.9 1.9 -0.1 0.2 -0.1 1.6 1.2 1.8 CA 1.9 1.5 0.9 1.9 1.9 1.9 0.9 1.3 -0.9 1.6 0.4 1.1 CC 2.8 1.8 2.2 2.2 2.2 2.2 2.2 2.2 0.4 1.9 1.7 1.4 X CU 2.7 1.6 2.0 2.1 2.1 2.1 2.0 2.0 0.3 1.8 1.5 1.2 GA 1.0 0.6 0.0 1.0 2.0 2.0 0.0 0.4 0.0 1.7 1.3 2.0 GG 1.8 1.3 0.7 1.8 2.4 2.4 0.7 1.1 0.0 2.1 1.2 1.9 GU 1.8 0.4 1.6 0.8 1.8 1.8 1.6 1.2 -2.0 1.5 -0.7 1.8 UC 2.7 1.6 2.0 2.1 2.1 2.1 2.0 2.0 0.3 1.8 1.5 1.2 UG 0.3 -1.1 0.1 0.7 0.3 0.3 0.1 0.3 -3.5 0.0 -2.2 0.3 UU 2.2 0.7 1.9 1.2 1.2 1.2 1.9 1.5 0.2 0.9 1.5 0.3

Figure 6: Free energies for all interior loops in RNA closed by a CG and an AU base pair. Values of `X' or `Y' that correspond to bases that could form Watson-Crick pairs have been removed for brevity.

                        5' ------> 3'
                         C \/ \_/ A
                         G /\  |  U
                       3' <------ 5'
 Y:   A    A    A    C    C    C    G    G    G    U    U    U  
      A    C    G    A    C    U    A    G    U    C    G    U  
 --------------------------------------------------------------
  AA 2.0  1.6  1.0  2.0  2.6  2.6  1.0  1.4  0.2  2.3  1.5  2.2
  AC 2.4  1.9  1.3  2.4  2.4  2.4  1.3  1.7 -0.4  2.1  0.8  1.5
  AG 0.9  0.4 -0.1  0.9  1.9  1.9 -0.1  0.2 -0.1  1.6  1.2  1.8
  CA 1.9  1.5  0.9  1.9  1.9  1.9  0.9  1.3 -0.9  1.6  0.4  1.1
  CC 2.8  1.8  2.2  2.2  2.2  2.2  2.2  2.2  0.4  1.9  1.7  1.4
X CU 2.7  1.6  2.0  2.1  2.1  2.1  2.0  2.0  0.3  1.8  1.5  1.2
  GA 1.0  0.6  0.0  1.0  2.0  2.0  0.0  0.4  0.0  1.7  1.3  2.0
  GG 1.8  1.3  0.7  1.8  2.4  2.4  0.7  1.1  0.0  2.1  1.2  1.9
  GU 1.8  0.4  1.6  0.8  1.8  1.8  1.6  1.2 -2.0  1.5 -0.7  1.8
  UC 2.7  1.6  2.0  2.1  2.1  2.1  2.0  2.0  0.3  1.8  1.5  1.2
  UG 0.3 -1.1  0.1  0.7  0.3  0.3  0.1  0.3 -3.5  0.0 -2.2  0.3
  UU 2.2  0.7  1.9  1.2  1.2  1.2  1.9  1.5  0.2  0.9  1.5  0.3

Some special rules apply to 2-loops. A stacked pair that occurs at the end of a helix has a different free energy than if it were in the middle of a helix. Because of the availability and precision of data, we distinguish between GC closing and non-GC closing base pairs. In particular, a penalty (terminal AU penalty) is assigned to each non-GC closing base pair in a helix. The value of this penalty is stored in the MISCLOOP file.

Because free energies are assigned to loops, and not to helices, there is no a priori way of knowing whether or not a stacked pair will be terminal or not. For this reason, the terminal AU penalty is built into the TSTACKH and TSTACKI tables. For bulge, multi-branch and exterior loops, the penalty is applied explicitly. In all of these cases, the penalty is formally assigned to the adjacent loop, although it really belongs to the helix.

A "Grossly Asymmetric Interior Loop (GAIL)" is an interior loop that is 1 × n, where n>2. The special "GAIL" rule that is used in this case substitutes AA mismatches next to both closing base pairs of the loop for use in assigning terminal stacking free energies from the TSTACKI file.

A k-loop, ${\bf L}$ , where k > 2, is called a multi-branch loop. It contains k-1 base pairs, and is closed by a k^th base pair. Thus there are k stems radiating out from this loop. Because so little is known about the effects of multi-branch loops on RNA stability, we assign free energies in a way that makes the computations easy. This is the justification for the use of an affine free energy penalty for multi-branch loops. The free energy, $δδG({\bf L})$ , is given by:

$\begin{displaymath} δδG({\bf L}) = a + b \times l_{s}({\bf L}) + c \times l_{d}({\bf L}) + δδG_{stack}, \end{displaymath}$

(6)

where a, b and c are constants that are stored in the miscloop file and $δδG_{stack}$ includes stacking interactions that will be explained below. This simple energy function allows the dynamic programming algorithm used by mfold to find optimal multi-branch loops in time proportional to n³. It would take exponentially increasing time (with sequence length) to use a more appropriate energy function derived from Jacobson-Stockmeyer theory [30] that grows logarithmically with $l_{s}({\bf L})$ . In the efn2 program that recalculates folding free energies using more realistic rules (defined below), equation 6 is replaced by:

$\begin{displaymath} δδG({\bf L}) = a + 6b + 1.75 \times RT \times \l... ...bf L})/6) + c \times l_{d}({\bf L}) + δδG_{stack}. \end{displaymath}$

(7)

That is, the linear dependence on l_s changes to a logarithmic dependence for more than 6 single stranded bases in a multi-branch loop.

Stacking free energies, $δδG_{stack}$ are computed for multi-branch and exterior loops. In the folding algorithm these are single strand stacking free energies, also known as dangling base free energies, because they are applied to single stranded bases adjacent to a base pair that is either in the loop, or closes the loop. This single stranded base may "dangle" from the 5' or 3' end of the base pair. These parameters are stored in a file named dangle.dg or dangle.TC, as above.

Figure 7 shows some single strand stacking free energies.

**Figure 7:** Free energies for all possible single stranded bases that are adjacent to a CG base pair. 'X' refers to column. Note that the 3' dangling free energies are larger in magnitude than the 5' dangling free energies.
X X ------------------ ------------------ A C G U A C G U ------------------ ------------------ 5' --> 3' 5' --> 3' CX C G GX 3' <-- 5' 3' <-- 5' -1.7 -0.8 -1.7 -1.2 -0.2 -0.3 0.0 0.0

If i.j and $j\!+\!2.k$ are 2 base pairs, then r_j+1 can interact with both of them. In this case, the stacking is assigned to only 1 of the 2 base pairs, whichever has a lower free energy (usually the 3'stack). If k.l is a base pair and both r_k-1 and r_l+1 are single stranded, then both the 5' and 3' stacking are permitted. The value of $δδG_{stack}$ is then the sum of all the single base stacking free energies associated with the base pairs and closing base pair of the loop.

It has been evident for some time that to make the free energy rules more realistic for multi-branch and exterior loops, and to improve folding predictions, we would be compelled to take into account the stacking interactions between adjacent helices. Two helices, $\bf H_{1}$ and $\bf H_{2}$ in a multi-branch or exterior loop are adjacent if there are 2 base pairs i.j and $j\!+\!1.k$ , i.j and $i\!+\!1.k$ or i.j and $k.j\!-\!1$ that close $\bf H_{1}$ and $\bf H_{2}$ , respectively. The last 2 cases can only occur in a multi-branch loop. In addition, we define almost adjacent helices as 2 helices where the addition of a single base pair (usually non-canonical), results in an adjacent pair. The concept of adjacent helices is important, since they are often coaxial in 3 dimensions, with a stacking interaction between the adjacent closing base pairs. The concept of almost adjacent comes from tRNA where, in many cases, the addition of a GA base pair at the base of the anti-codon stem creates a helix that is adjacent to, and stacks on, the D-loop stem.

Mfold does not yet take into account coaxial stacking of adjacent or almost adjacent helices. The efn2 program that re-evaluates folding energies based on our best estimates does take this into account. It is not a trivial matter to decide which combination of coaxial stacking and single base stacking gives the lowest free energy in a multi-branch or external loop, and a recursive algorithm is employed to find this optimal combination. For example, coaxial stacking excludes single base stacking adjacent to the stacked helices. Free energies for the stacking of adjacent helices are stored in a file called coaxial.dg. The format is the same as for stack.dg. When 2 helices are almost adjacent, then 2 files, named coaxstack.dg and tstackcoax.dg are used. The format is the same as for stacking free energies. 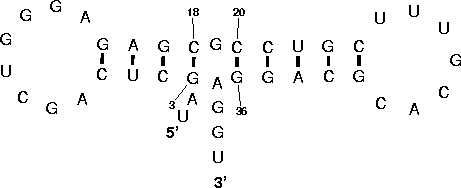The use of these 2 files is explained with the aid of Figure 8. Thus, in the efn2 program, δδG_stack is a combination of single base stacking and coaxial stacking, depending on the loop.

**Figure 8:** The helices closed by G³-C¹⁸ and C²⁰-G³⁶ are almost adjacent. Their stacking is mediated by a non-canonical G¹⁹-A³⁷ base pair. The free energy for the G¹⁹-A³⁷ to C²⁰-G³⁶ comes from the `tstackcoax.dg` file. This is used where the phosphate backbone is unbroken, since there are 2 covalent links. The C¹⁸-G³ to G¹⁹-A³⁷ stacking free energy comes from the `coaxstack.dg`, which is used for stacking where the backbone is broken. In this case, G³ and A³⁷ are not linked.
$\begin{figure}\centering \epsfig{file=figure.2dps,width=0.9\textwidth} \end{figure}$

In the case of circular RNA, the choice of origin is arbitrary. However, once it is made, what would be the exterior loop in linear RNA becomes equivalent to a hairpin, bulge, interior or multi-branch loop, or a stacked pair.

The Turner parameters for RNA folding have been published and summarized a number of times. The most significant older publications are [31,32,33], and mfold was originally used these results alone. Version 1 of mfold had no tloop.dg file, and there was a single terminal stacking free energy file, tstack.dg. Tetraloop bonus free energies were added in version 2.0. The tstack file was split into 2 files in version 2.2. Version 3.0 introduces triloop bonus energies, and both tetraloop and triloop bonus energies now depend on the closing base pair. Special rules for small interior loops are also new. For example, the 2 × 2 interior loop rules have evolved from [34]. Coaxial stacking was also introduced in version 3.0, although it's importance was realized eariler [35].

A complete set of DNA folding parameters have recently become available [36]. These are based on measuremments for stacking and mismatches, and on the literature for loop and other effects. Parameters are also available for predicting the formation of RNA/DNA duplexes [37].

Next: Constrained folding Up: Algorithms and Thermodynamics for Previous: Software platforms and environment

Michael Zuker
Center for Computational Biology
Washington University in St. Louis
1998-12-05