Introduction


Next: Applications Up: Using Reliability Information to Previous: Abstract
Introduction
The development of sub-optimal algorithms for RNA secondary structure prediction [Williams & Tinoco, 1986,Zuker, 1989b,Zuker, 1989a] helped to mitigate the uncertainty of predicting a secondary structure of a single RNA sequence from thermodynamic data. The mfold algorithm [Zuker, 1989a,Zuker, 1994] predicts suboptimal foldings as well as an ``energy dot plot'', which is a dot plot showing all possible base pairs that can participate in foldings within a specified increment of the predicted minimum folding energy. The collection of sub-optimal folding predictions and, in the case of the Zuker algorithm, the energy dot plot, combine to give the user an idea of how well determined a given prediction is.
A number of heuristic descriptors have been developed in conjunction with the mfold package that describe the propensity of individual bases to participate in base pairs and whether or not a predicted helix is ``well determined''. These descriptors are P-num , S-num and H-num. The first 2 were introduced early [Jaeger et al., 1989,Jaeger et al., 1990], and are computed for individual bases.
P-num is defined from the energy dot plot, and therefore depends on
an (arbitrary) energy increment and whether or not the dot plot has been filtered to
eliminate isolated base pairs or short helices. For the 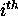 base in a molecule with n bases,
base in a molecule with n bases, 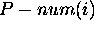 is the total number of dots in the
is the total number of dots in the 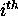 row and column of the dot plot. In simple words,
row and column of the dot plot. In simple words, 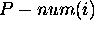 is the total number of different base pairs that can be formed
using the
is the total number of different base pairs that can be formed
using the 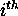 base in all foldings within the
prescribed energy increment. If
base in all foldings within the
prescribed energy increment. If 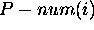 is large,
and this is a relative term, then the
is large,
and this is a relative term, then the 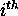 base is promiscuous in its association with other bases. We say that it is ``poorly
determined''. In an ensemble of foldings, it will be single stranded or paired with
many different bases. In a particular folding, we cannot say with any certainty how
this base will pair. If
base is promiscuous in its association with other bases. We say that it is ``poorly
determined''. In an ensemble of foldings, it will be single stranded or paired with
many different bases. In a particular folding, we cannot say with any certainty how
this base will pair. If 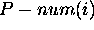 is 0, then the
is 0, then the
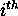 base must be single stranded.
Otherwise, P-num gives no information of the propensity to be single stranded. This is
furnished by S-num, defined next.
base must be single stranded.
Otherwise, P-num gives no information of the propensity to be single stranded. This is
furnished by S-num, defined next.
S-num is defined from a collection of optimal and suboptimal
foldings, and is thus independent from any dot plot computations. In a group of
m foldings, 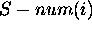 is the number of
foldings in which base i is single-stranded, divided by m. Thus
is the number of
foldings in which base i is single-stranded, divided by m. Thus
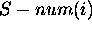 is a sample probability that the
is a sample probability that the
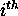 base is single-stranded. A value of S-num
that is close to 0 or 1 is ``good'' in the sense that it tells us with a
high degree of confidence whether the base is paired, or not paired, respectively. We
say that a base is ``well-determined'' if S-num is near 1 (almost certainly
single stranded) or if S-num is near 0 (almost certainly base paired) and P-num
is low.
base is single-stranded. A value of S-num
that is close to 0 or 1 is ``good'' in the sense that it tells us with a
high degree of confidence whether the base is paired, or not paired, respectively. We
say that a base is ``well-determined'' if S-num is near 1 (almost certainly
single stranded) or if S-num is near 0 (almost certainly base paired) and P-num
is low.
At a later date [Zuker & Jacobson,
1995], we introduced the notion of H-num, which is an extension of P-num to
helices. For a singe base pair, 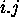 , we
define
, we
define 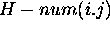 to be
to be 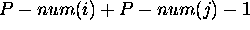 . This is simply the total number of base pairs that can be formed
using the
. This is simply the total number of base pairs that can be formed
using the 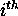 or
or 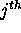 bases, in all foldings within the chosen energy increment. For a
helix, H-num is the average of these values for all the base pairs in the helix.
Helices with relatively low H-num values are said to be ``well-determined'' and those
with relatively high values are said to be ``poorly determined''. We used the H-num
measure to demonstrate that ``well-determined'' helices in optimal foldings are more
likely to be correct than ``poorly determined'' ones [Zuker & Jacobson, 1995]. It is worth adding here that a
``well-determined'' helix does not have to be in an optimal folding.
bases, in all foldings within the chosen energy increment. For a
helix, H-num is the average of these values for all the base pairs in the helix.
Helices with relatively low H-num values are said to be ``well-determined'' and those
with relatively high values are said to be ``poorly determined''. We used the H-num
measure to demonstrate that ``well-determined'' helices in optimal foldings are more
likely to be correct than ``poorly determined'' ones [Zuker & Jacobson, 1995]. It is worth adding here that a
``well-determined'' helix does not have to be in an optimal folding.
The recursive computation of rigorous partition functions for the RNA
secondary structure model [McCaskill, 1990] lead to
the development of rigorous statistics to describe uncertainties in RNA folding
predictions. The original work computes base pair probabilities and, as a direct
consequence, probabilities that any base will be single or double stranded. Base pair
probabilities are plotted in what is called a ``boxplot''. This is similar to the
mfold energy dot plot, except that base pairs are plotted as black squares whose
areas are proportional to the probability of that base pair. There is a probability
cutoff, usually 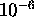 , below which base pairs
are not plotted. These ideas have been taken up and expanded on by a theoretical
chemistry group at the University of Vienna. The resulting software has become to be
known as the ``Vienna (RNA) package'' [Hofacker et al., 1994].
, below which base pairs
are not plotted. These ideas have been taken up and expanded on by a theoretical
chemistry group at the University of Vienna. The resulting software has become to be
known as the ``Vienna (RNA) package'' [Hofacker et al., 1994].
Although an experienced user of the mfold package can extract information relatively easily from the dot plot superposition of optimal and sub-optimal foldings, we find that a color annotation of individual foldings simplifies the interpretation of the results that are obtained from these plots. The major innovation described in this work is the annotation of foldings with ``well-definedness'' information. The latter can be the P-num, S-num or H-num measures computed from the current mfold package, or base pair probabilities and other measures as computed by the Vienna package.
Our annotation method was developed to annotate predicted secondary structures. However, structural models that have been created from comparative sequence analysis can also be annotated.
In addition to color we also use another form of annotation to show how closely two structural models are related to one another. The short line segments that denote base pairs in a structure plot can be thickened to denote base pairs that are conserved in a reference folding. This feature can be used to visualize conformational differences between wild-type and mutant genomes, between predicted alternative foldings, and between the phylogenetic and predicted models of an RNA molecules. The application of these approaches to the analysis of several molecules of RNase P RNA and 16S rRNA are given below.


Next: Applications Up: Using Reliability Information to
Previous: Abstract
 |
Michael Zuker Institute for Biomedical Computing Washington University in St. Louis August 21 1998. |